Sau kỳ thi tốt nghiệp trung học phổ thông quốc gia, kỳ thi quyết định tương lai của nhiều sĩ tử 2k4. Thay vì lo lắng vô ích không có kết quả, sao các bạn không thử tìm hiểu trước các thông tin về toán 12, để có thể chuẩn bị cho mình một tâm lý, kiến thức vững chắc. Sau đây là lời hướng dẫn cách bấm máy tính nguyên hàm đơn giản trên các dòng máy Casio fx 580 VNX và 570VN.
Cách bấm máy tính nguyên hàm chỉnh máy tính
Để có thể bấm máy tính ra kết quả có sai số nhỏ nhất, các bạn cần chỉnh máy tính về các chế độ sau.
Bấm: Shift – Mode – 9 chỉnh máy tính về sai số nhỏ 9 chữ số thập phân
Bấm: Shift – Mode – 4 chỉnh máy tính về đơn vị góc là Radian
Cách bấm máy tính nguyên hàm dạng thứ nhất
Tìm nguyên hàm F(x)của hàm số f(x)
Cú pháp nhập máy tính:
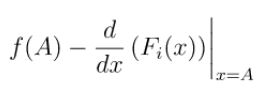
Trong đó:
- f (A): giá trị của f(x) tại x = A (A là hằng số bất kỳ thuộc tập xác định và A lấy giá trị nhỏ 0.1; 0.2; 0.3; 0.4; …; 1; 1.1)
- Fi(x): các kết quả nguyên hàm.
Ví dụng vận dụng
Ví dụ 1: 5(x2 + x )2x + 1 dx; x > -12 bằng
- (x2+x+1)2x+1+C
- (x2 – x+1)2x+1+C
- (x2+x – 1)2x+1+C
- (x2 – x – 1)2x+1+C
Đáp án C
Lời giải
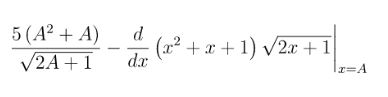
- Bước 1: nhập phương trình
- Bước 2: Gán x = A = 1 hoặc 0,1 ( bấm CALC → A) cho kết quả không bằng 0 ta loại ngay đáp án đó ⇒ Loại A
- Thay Fi (x) bằng đáp án B và gán A như trên ta nhận kết quả khác 0 ⇒ Loại B
- Thay Fi (x) bằng đáp án C và gán A như trên ta nhận kết quả bằng 0; để chắc chắn đúng ta nên kiểm tra thêm vài giá trị của A như 0; 0,2; 0,5; 1 ⇒ Chọn C. ( Không nên gán x = A giá trị quá lớn máy sẽ không ra đáp án đấy)
Ví dụ 2: x.sinx.cosx dx bằng
- A.12 (14sin2x – x2cos2x) + C
- -12 (14sin2x – x2cos2x) + C
- 12 (14sin2x + x2cos2x) + C
- – 12 (14sin2x + x2cos2x) + C
Đáp án A
Lời giải
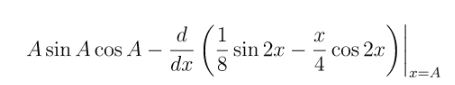
- Nhập phương trình:
- Gán A = 0,1 Cho kết quả bằng 0 – kiểm tra lại bằng vài giá trị khác như 0,2; 0,3; 0,5 ta nhận kết quả đều bằng 0 ⇒ Chọn A.
Ví dụ 3: – 2 x(1 + In x)2 dx (x>0) bằng
- F(x)= 1 + In x1 – In x +C
- F(x)= 1 – In x1 + In x +C
- F(x)= – 1 + In x1 + In x +C
- – 12
Đáp án B
Lời giải
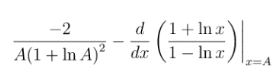Gán A = 0,1 nhận kết quả khác ⇒ A không là kết quả của bài
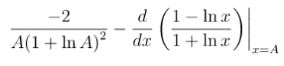Gán A = 0,1 ra kết quả bằng 0 ⇒ B là đáp án cần tìm
Cách bấm máy tính nguyên hàm dạng thứ hai
Tìm 1 nguyên hàm F(x) của hàm số f(x) biết F(x0)= M
Cú pháp nhập máy tính: Fi(A) – M – X0Af(x)dx
Ví dụ vận dụng
Ví dụ 1: Tìm nguyên hàm F(x) của hàm số fx=x3+3×2+x – 1 x2+2x+1 biết f1=13
- A.x22+x+2x+1-613
- x22+x+2x+1
- x22+x+2x+1+613
- x22+x+2x+1-136
Đáp án D
Lời giải
- Nhập: A22+A+2A+1-613-1Ax3+3×2+x – 1 x2+2x+1 Gán A = 0,1 và 1 đều nhận kết quả khác 0 ⇒ A không là kết quả
- Nhập : A22+A+2A+1-136-1Ax3+3×2+x – 1 x2+2x+1 Gán A = 0,1 và 1 đều nhận kết quả bằng 0 ⇒ D là kết quả cần tìm.
Ví dụ 2: Tìm nguyên hàm F(x) của hàm số fx=5 5sin x + 3 cos x + 3 thỏa f2=3 In 2
- A.Fx=3In5 tan x2 – 3
- Fx=In5 tan x2 +3
- Fx=In5 tan x2 – 3 + 2 In 2
- Fx=3In5 tan x2 + 3
Đáp án B
Lời giải:
- Nhập 3In5 tan x2 – 3 – 3 In 2 2A5 5sin x + 3 cos x + 3dx Gán A = 0; 0,1 nhận được kết quả khác 0 ⇒ loại đáp án A
- Nhập In5 tan x2 – 3 – 3 In 2 2A5 5sin x + 3 cos x + 3dx Gán A = 0; 0,1 nhận được kết quả là số 0 ⇒ nhận đáp án B
Cách bấm máy tính nguyên hàm dạng thứ 3
Tính tích phân: abf(x)dx
Trong các đáp án đều là số dạng vô tỷ: dạng số của căn, số e, số pi các bạn nên bấm lưu để ghi nhận lại kết quả
Cú pháp nhập máy: abf(x)dx
Ví dụ vận dụng
Ví dụ 1: 25(3x-4)4dx bằng
- A.8972027
- 19892720
- 96002518
- 16101915
Đáp án D
Ví dụ 2: 1ex2 In dx bằng
- A.e2+ 14
- 2e3+ 19
- 3e3+ 28
- 2e3+ 33
Đáp án B
- Ta có: e2+ 14 ≈ 2,097264025
- Ta có: 2e3+ 19 ≈ 4,574563716
- Ta có: 3e3+ 28 ≈ 7,782076346
- Ta có: 2e3+ 33 ≈ 5, 926037399
Ví dụ 3: 02sin 2xcos2x + 4sin2xdx bằng
- A.32
- 34
- 23
- 25
Đáp án C
Ví dụ 4: 04sin ( x – 4 )dx sin 2x + 2(1 + sin x + cos x)
- A.4 – 324
- 4 + 324
- 4 + 323
- 4 – 323
Đáp án A
Lời kết
Bài viết trên đã hướng dẫn các bạn cách bấm máy tính nguyên hàm cùng những ví dụng minh họa dễ hiểu nhất. Mong rằng các bạn có thể nắm rõ kiến thức và áp dụng dễ dàng vào các bài thi sắp tới.