Hình thoi là một hình học phẳng có bốn cạnh bằng nhau và đối diện với nhau. Trong bài viết này, chúng ta sẽ tìm hiểu về đặc điểm, dấu hiệu nhận biết hình thoi, cùng với công thức tính chu vi và diện tích của hình thoi. Cùng với đó sẽ tìm hiểu về ứng dụng các kiến thức này trong cuộc sống như thế nào.
XEM THÊM:
- Viết chương trình tính tổng S=1+2+3+…+n trong python và ví dụ
- Cách Vẽ Bìa Sách Đẹp, Đơn Giản, Dễ Vẽ Chỉ Trong 5 Phút
Định nghĩa hình thoi là gì?
Hình thoi là một hình tứ giác có 4 cạnh bằng nhau, đồng thời có 2 cặp cạnh đối diện song song với nhau và cặp góc đối bằng nhau. Hình thoi có hai đường chéo, mỗi đường chéo chia tứ giác thành hai cặp tam giác đồng dạng.
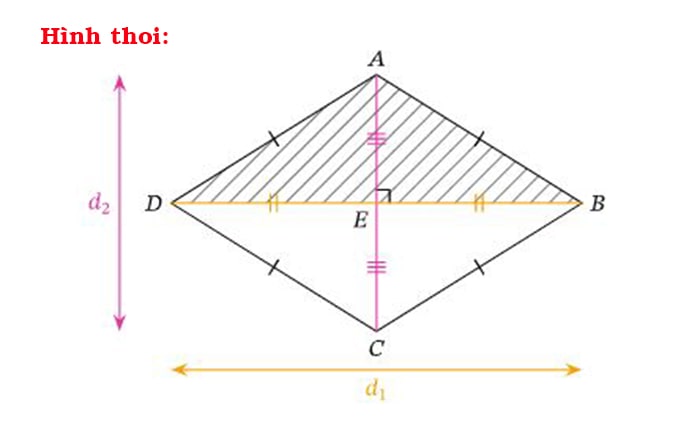
Đặc điểm, dấu hiệu hình thoi là gì?
Đặc điểm của hình thoi bao gồm:
- Có bốn cạnh bằng nhau
- Có hai đường chéo chéo qua tâm hình thoi và vuông góc với nhau
- Có đôi một hai góc đối diện bằng nhau
- Tổng độ dài hai cạnh kề bằng độ dài tổng hai cạnh còn lại
Để nhận biết một hình thoi, chúng ta có thể sử dụng các dấu hiệu sau:
- Có bốn cạnh bằng nhau.
- Có 2 đường chéo vuông góc tức có 2 đường chéo là đường trung trực của nhau.
- Có 2 cặp góc đối diện bằng nhau.
Công thức tính chu vi hình thoi và ví dụ
Chu vi của một hình thoi là tổng độ dài của bốn cạnh, do có 4 cạnh bằng nhau với độ dài là a thì công thức tính chu vi của hình thoi bằng tích 4 lần cạnh hình thoi: P = 4*a.
Ví dụ: Cho hình thoi có cạnh của hình thoi là 8 cm, Tính chu vi hình thoi?
Đáp số: Ta có thể áp dụng công thức tính chu vi bằng công thức P = 4 * a = 4 * 8 = 32 cm.
Công thức tính diện tích hình thoi và ví dụ
Diện tích hình thoi bằng một nửa của tích hai đường chéo: S = (d1 * d2)/2, trong đó d1 và d2 là độ dài của hai đường chéo.
có thể nói: Diện tích hình thoi bằng tích của chiều cao và cạnh hình thoi. S = h * a, trong đó h là chiều cao; a là cạnh của hình thoi.
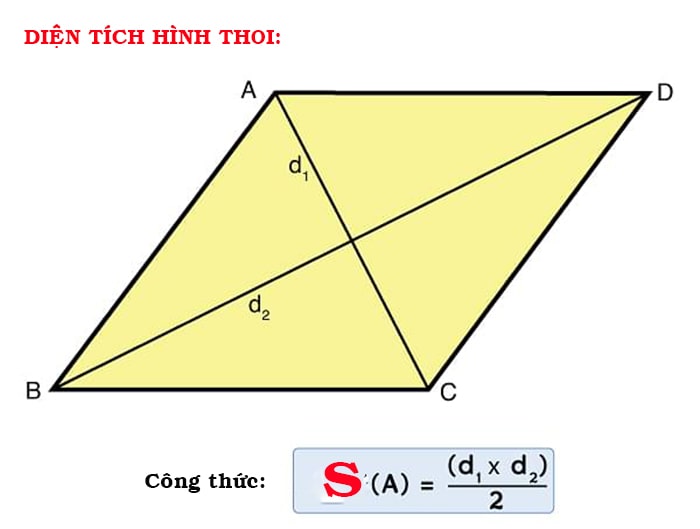
Ví dụ: Cho một hình thoi có đường chéo lớn có độ dài là 8 cm, và đường chéo bé là 4 cm, ta có thể tính diện tích bằng công thức S = (8 * 4)/2 = 16 cm^2.
Các dạng bài tập về hình thoi cần chú ý
Các bạn học sinh cần chú ý một số dạng bài tập về hình thoi như sau:
- Bài tập về tính diện tích hình thoi
- Bài tập về tính chu vi hình thoi
- Bài tập về tính góc trong hình thoi.
- Bài tập về tính đường cao hình thoi
- Bài tập về chứng minh các dấu hiệu nhận biết hình thoi.
Các bạn học sinh để giải các bài tập về hình thoi, các bạn cần nắm vững các kiến thức định nghĩa, đặc điểm và công thức về hình thoi.
Ứng dụng của hình thoi trong cuộc sống?

Hình thoi được sử dụng trong nhiều lĩnh vực khác nhau trong cuộc sống hàng ngày. Một số ví dụ bao gồm:
- Trong toán học, hình thoi là một trong những hình học căn bản được giảng dạy cho học sinh.
- Trong xây dựng, kiến trúc hình thoi được sử dụng để thiết kế các mặt tiền, các góc cạnh của tòa nhà, lát nền tạo hoa văn bắt mắt,…
- Trong công nghệ, hình thoi được sử dụng để mã hoá thông tin và giải mã mật khẩu.
- Trong ngành cơ khí, sản xuất công nghiệp, hình thoi được sử dụng để thiết kế các chi tiết cơ khí, đặc biệt là trong các máy móc và thiết bị.
Trong bài viết này, Tingenz đã giới thiệu về định nghĩa hình thoi, đặc điểm, công thức từ đó có thể rút ra dấu hiệu nhận biết hình thoi. Các bạn muốn làm bài tập đúng và ứng dụng của nó trong cuộc sống thì cần nắm vững các kiến thức đó. Chúc các bạn luôn học tốt !
