Công thức tính độ dài đoạn thẳng là kiến thức quan trọng được áp dụng ở nhiều cấp bậc trong lớp học đến ứng dụng trong cuộc sống. Chính vì thế bài viết xin được gửi tới các bác bài học quan trọng này bao gồm khái niệm, công thức và bài tập chi tiết có lời giải để các bạn học sinh hiểu rõ và sâu hơn.
XEM THÊM:
- Hình thoi là gì? Chu vi, diện tích, dấu hiệu nhận biết và ví dụ
- Viết chương trình tính tổng S=1+2+3+…+n trong python và ví dụ
Định nghĩa độ dài của một đoạn thẳng
Độ dài của một đoạn thẳng là khoảng cách nối giữa hai điểm hoặc Độ dài đoạn thẳng là một giá trị số đo lường khoảng cách giữa hai điểm trên một đường thẳng. Nó cho biết độ dài của phần đường thẳng nối hai điểm đó.
Đơn vị đo lường độ dài thường dùng là: mm, cm, dm, m, km.
Công thức tính độ dài đoạn thẳng AB

Trong mặt phẳng
Độ dài đoạn thẳng là khoảng cách giữa hai điểm A(x1,y1) và B(x2,y2), được ký hiệu là AB. Công thức tính độ dài đoạn thẳng thẳng AB bằng căn bậc hai của tổng bình phương của hiệu giữa các tọa đọa x,y của 2 điểm A và B.
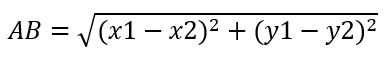
Trong đó:
- x1 và y1 là tọa độ của điểm A
- x2 và y2 là tọa độ của điểm B
Trong không gian 3 chiều
Để tính độ dài đoạn thẳng AB trong không gian ba chiều, ta sử dụng công thức sau:
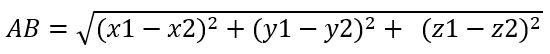
Trong đó:
- A(x1, y1, z1) là tọa độ điểm A trong không gian ba chiều.
- B(x2, y2, z2) là tọa độ điểm B trong không gian ba chiều.
Công thức tính độ dài đoạn thẳng bằng căn bậc hai của tổng bình phương của hiệu giữa các tọa độ x, y, và z của hai điểm A và B.
Bài tập tính độ dài đoạn thẳng có lời giải chi tiết
Bài tập 1: Cho đoạn thẳng AB, biết A(2, 3) và B(5, 7). Tính độ dài đoạn thẳng AB.
Lời giải:
Để tính độ dài đoạn thẳng AB, ta sử dụng công thức khoảng cách:
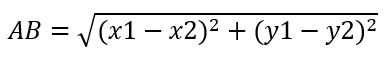
Với A(2, 3) và B(5, 7), ta thay các giá trị vào công thức:
AB = √((5 – 2)² + (7 – 3)²)
= √(3² + 4²)
= √(9 + 16)
= √25
= 5
Vậy độ dài đoạn thẳng AB là 5 đơn vị độ dài..
Bài tập 2: Cho đoạn thẳng CD, biết C(-2, 1) và D(3, 5). Tính độ dài đoạn thẳng CD.
Lời giải:
Để tính độ dài đoạn thẳng CD, ta sử dụng công thức khoảng cách Euclid:
CD =
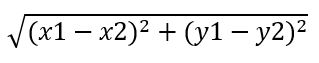
Với C(-2, 1) và D(3, 5), ta thay các giá trị vào:
CD = √((3 – (-2))² + (5 – 1)²)
= √(5² + 4²)
= √(25 + 16)
= √41
Vậy độ dài đoạn thẳng CD là √41 đơn vị độ dài.
Bài tập 3: Cho điểm A(-3, 2) và điểm B(7, -5). Hãy tính độ dài đoạn thẳng AB.
Lời giải:
Để tính độ dài đoạn thẳng AB, ta có:
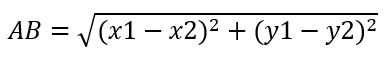
Thay vào đó với A(-3, 2) và B(7, -5):
AB = √((7 – (-3))² + (-5 – 2)²)
= √((7 + 3)² + (-5 – 2)²)
= √(10² + (-7)²)
= √(100 + 49)
= √149
Vậy độ dài đoạn thẳng AB là √149 đơn vị độ dài.
Bài tập 4: Cho điểm A(1, 2, 3) và điểm B(4, 5, 6). Hãy tính độ dài đoạn thẳng AB.
Lời giải:
Để tính độ dài đoạn thẳng AB trong không gian ba chiều, ta sử dụng công thức:
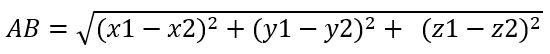
Thay vào đó với A(1, 2, 3) và B(4, 5, 6):
AB = √((4 – 1)² + (5 – 2)² + (6 – 3)²)
= √(3² + 3² + 3²)
= √(9 + 9 + 9)
= √27
= 3√3
Vậy độ dài đoạn thẳng AB trong không gian ba chiều là 3√3 đơn vị đo độ dài
Cách tính độ dài đoạn thẳng trong thực tế
Trong thưc tế ta có thể sử dụng một số cách sau đây:
- Dùng thước kẻ: Đây là cách đơn giản nhất để tính độ dài đoạn thẳng. Ta chỉ cần đặt thước kẻ song song với đoạn thẳng và đọc số đo trên thước.
- Sử dụng máy đo khoảng cách: Đây là cách chính xác hơn so với cách dùng thước kẻ. Máy đo khoảng cách có thể đo được độ dài của các vật thể ở xa, không cần phải tiếp xúc với chúng.
- Trong các công trình thực tế, có thiết kế bản vẽ thì chúng ta vấn sử dụng công thức trong tính độ dài đoạn thẳng

Ứng dụng của tính độ dài đoạn thẳng trong đời sống
Công thức để tính độ dài đoạn thẳng là một công cụ quan trọng trong đời sống, nó được sử dụng để giải quyết nhiều vấn đề liên quan đến khoảng cách hay định vị trong không gian. Ví dụ như trong đo đạc, xây dựng, thiết kế hoặc cả trong các bài toán hình học cơ bản. Công thức này cũng được sử dụng trong các ngành khác như vật lý, toán học và kỹ thuật. Việc tính độ dài đoạn thẳng rất hữu ích và quan trọng trong nhiều lĩnh vực khác nhau của đời sống.
Tingenz đã chia sẻ dầy đủ thông tin kiến thức quan trọng về tính độ dài đoạn thẳng và ví dụ. Mong rằng các bạn sẽ nắm vững và áp dụng chính xác công thức. Chúc các bạn học tập vui vẻ!
